W poprzednich odcinkach cyklu napisałem, że tak dla krzywych Béziera, jak i B-Spline każdy punkt kontrolny ma zdefiniowaną ?siłę przyciągania? tej krzywej. W przypadku krzywej Béziera dla każdej wartości parametru u ?siła? ta jest ustalona dla każdego z punktów kontrolnych Pi i jest ona większa od 0 dla każdego punktu krzywej pomiędzy jej początkiem a końcem. Dlatego modyfikacja jednego punktu kontrolnego wpływa na kształt całej krzywej
Funkcje definiujące to przyciąganie (Basis Functions) zależą od stopnia krzywej Béziera (liczby punktów kontrolnych), a ich wartości nie mogą być modyfikowane. Podobnie dla krzywej B-Spline dla każdej wartości parametru u jest określona siła przyciągania punktu krzywej C(u) przez każdy z jej punktów kontrolnych, ale dla zadanej wartości parametru u jest ona większa od 0 tylko dla ?niektórych? punktów kontrolnych Pi. Każdy punkt kontrolny krzywej B-Spline wpływa na jej kształt ?w obszarze najbliższym? punktowi Q(u) i nie wpływa w ogóle lub ?w stopniu bardzo małym? na tą część krzywej, która jest ?daleko? od niego. Dlatego modyfikacje punktów kontrolnych krzywej typu B-Spline mają charakter lokalny. Czy jednak można poprzestać na określeniach typu ?niektóre?, ?w obszarze najbliższym? lub ?daleko?? Myślę, że są one mało precyzyjne i wymagają bardziej szczegółowego wyjaśnienia.
Na każdej krzywej B-Spline, jako krzywej sklejonej z kilku krzywych cząstkowych istnieją punkty wspólne tych krzywych, czyli węzły (ang. knot). Zazwyczaj nie są one widoczne, bo większość algorytmów stosowanych w systemach CAD nie pozwala na bezpośrednią modyfikację tych punktów. Jeśli węzły mają rozkład równomierny (ang. uniform), czyli ich położenie na krzywej B-Spline jest opisane liniową stałymi przyrostami parametru u, to takie krzywe noszą nazwę UPBS (Uniform Polynomial B-Spline). Inaczej mówiąc każda cząstkowa krzywa Béziera krzywej typu B-Spline ma taką samą długość mierzoną przyrostem parametru ?u = ui+1 – ui. Zakres zmian tego parametru oraz jego wartości w węzłach mogą być dowolne, bo istotna jest tu równomierność przyrostów pomiędzy kolejnymi węzłami krzywej sklejanej (Rys. 1). Na przykład dla krzywej sklejonej z 4 segmentów każdy z następujących rozkładów jest równomierny: [-2,-1,0,1,2], [0, 0.25, 0.5, 0.75, 1], [1,5,9,13,17].
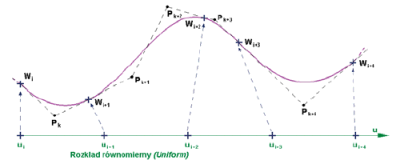
RYS. 1
Słowo Polynomial (wymierny) w nazwie Uniform Polynomial B-Spline odnosi się do standardowych wartości funkcji wagowych, które dla krzywej BSpline (podobnie jak dla krzywej Béziera) są opisane funkcjami wymiernymi (wielomianami). Jednak dla krzywej typu B-Spline ?siła przyciągania? krzywej przez każdy punkt kontrolny ma wartości różne od 0 tylko w pewnych zakresach parametru u, a nie jak dla krzywej Béziera ? na całej długości krzywej. Dla rozkładu równomiernego funkcje wagowe krzywej B-Spline mają dla każdego punktu kontrolnego identyczne wykresy, ale przesunięte o stałą wartość ?u, czyli o długość cząstkowej krzywej Béziera liczoną w przestrzeni parametru u. Jeśli B-Spline zbudowano z krzywych Béziera stopnia d°=3 (Rys. 2), to współrzędne dowolnego punktu tej krzywej Q(u) są zdeterminowane tylko przez 4 (a nie wszystkie!) punkty kontrolne… i to jest wyjaśnienie zastosowanego wcześniej określenia ?niektóre?. Warto też zauważyć, że wpływ dwóch (?środkowych?) punktów kontrolnych (Pk-1 i Pk) na kształt krzywej jest znaczny, a pozostałych dwóch (?skrajnych?) jest znikomy (<1/6).Ponadto z Rys. 2 wynika jasno, że każdy punkt kontrolny ma wpływ na 4 kolejne krzywe cząstkowe i to jest właściwe wyjaśnienie określenia ?w obszarze najbliższym?.
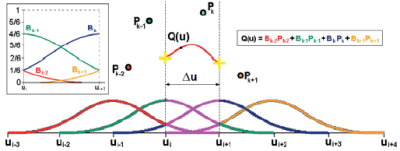
RYS. 2
Taki równomierny rozkład węzłów nie zawsze jest jednak najlepszy ? tak dla spełnienia wymagań konstrukcyjnych (kształt, ciągłość), jak dla zapewnienia optymalnego modelu matematycznego.
Po pierwsze dlatego, że punkty skrajne krzywej typu UPBS (rozkład równomierny) nie pokrywają się z pierwszym i ostatnim punktem kontrolnym krzywej. A to jest oczywiście sprzeczne z logiką konstrukcyjną, bo definicja krzywej typu B-Spline polega zazwyczaj na wskazaniu jej kolejnych punktów węzłowych (także punktu początkowego i końcowego). Po drugie dlatego, że nie zawsze jednakowe przyrosty ?u pomiędzy kolejnymi węzłami krzywej B-Spline są rozwiązaniem gwarantującym optymalną definicję krzywej ? tak z punktu widzenia jej modelu matematycznego, jak i kształtu krzywej. I wreszcie, po trzecie ? bo czasami konstruktor potrzebuje takiej krzywej, która we wskazanym punkcie ma ciągłość niższą niż G2. We wszystkich tych przypadkach stosujemy różne długości parametryczne krzywych cząstkowych oraz powtórzenia punktów kontrolnych ? kilka kolejnych punktów kontrolnych ma takie same współrzędne. Powtarzanie punktów kontrolnych krzywej B-Spline wpływa nie tylko na zakres krzywej, na który mają wpływ te punkty, ale także na równanie funkcji wagowej, w tym na jej wartość maksymalną. Z powodów opisanych powyżej algorytmy definiowania krzywych w systemach CAD ?naruszają? równomierność krzywych UPBS i tworzą wielomianowe krzywe nierównomierne (Rys. 3), w skrócie NUPBS (Non-Uniform Polynomial B-Spline).
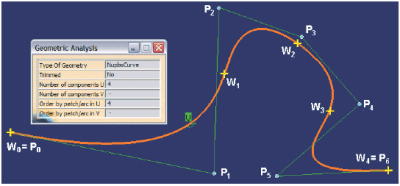
RYS. 3
Jeśli dla rozkładu nierównomiernego długości krzywych cząstkowych są różne od ?u, to punkty kontrolne mogą mieć wpływ na części krzywej o różnej długości. Nierównomierność rozkładu węzłów krzywej B-Spline wpływa więc na ?szerokość? odpowiednich zakresów krzywej, na które mają wpływ poszczególne punkty kontrolne. A to oznacza, że nierównomierność rozkładu węzłów wpływa na szerokość tego zakresu, który wcześniej nazwałem ?obszarem najbliższym? danemu punktowi kontrolnemu.
RYS. 4
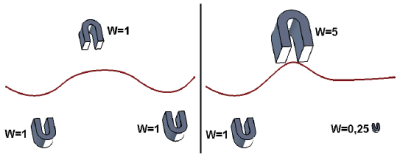
Pozostaje jeszcze jedno pytanie, na które nie podałem odpowiedzi: czy można zmieniać wartości funkcji bazowych punktów kontrolnych lub inaczej: czy można zmienić wagi ? z jakimi punkty kontrolne ?przyciągają? krzywą sklejaną ? w taki sposób by uzyskać efekt pokazany na Rys. 4? Wyjaśnienie tego problemu rozpocznijmy od omówienia krzywych stożkowych (d°=2), których kształt jest wyznaczony przez 3 punkty kontrolne i parametr p. W zależności od tego, jaką wartość ma ten parametr krzywa może być elipsą, parabolą lub hiperbolą (Rys. 5). Przez analogię można przyjąć, że parametr p jest proporcjonalny do ?wagi?, z jaką punkt kontrolny P1 ?przyciąga? definiowaną krzywą.
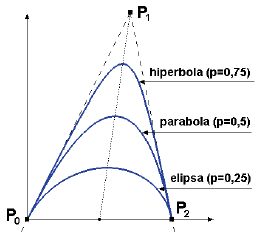
RYS. 5
Jeśli funkcję bazową każdego punktu kontrolnego krzywej B-Spline podzielimy przez kolejną funkcję, która jest proporcjonalna do siły przyciągania krzywej przez ten punkt kontrolny, to uzyskamy krzywą wymierną (ang. Rational).
Na przykład (Rys. 6) dla W=0 punkt P2 nie ?przyciąga? krzywej, dla W=1 wartość ?wagi? jest standardowa, a dla W>1 ten wpływ jest większy niż dla standardowej wartości funkcji bazowej ? krzywa jest znacznie bliżej punktu kontrolnego. W konsekwencji, jeśli dla krzywej typu B-Spline połączymy cechy nierównomierności i wymierności, to uzyskamy krzywą typu NURBS (Non-Uniform Rational B-Spline). Krzywa tego typu ma oczywiście wszystkie opisane wcześniej własności krzywych B-Spline oraz dodatkową możliwość lokalnych modyfikacji krzywej uzyskaną dzięki wprowadzeniu dodatkowego ?współczynnika wagi? punktu kontrolnego. Na Rys. 7 pokazano krzywą typu NURBS z różnymi ?wagami? punktu P1 (W1=1 i W1=10).
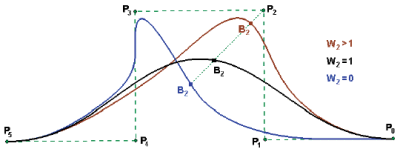
RYS. 6
Na zakończenie trzeba dodać, że krzywa typu B-Spline lub NURBS, w odróżnieniu od krzywych Béziera, mogą mieć ciągłość G2, G1 lub nawet G0. Przypadek ciągłości typu G0 nabiera szczególnego znaczenia w przypadku definiowania krzywych stylistycznych, kiedy intencją konstruktora jest uzyskanie ?ostrego? wierzchołka na krzywej, a potem ?ostrej? krawędzi na modelu powierzchniowym ?rozpiętym? na takiej krzywej.
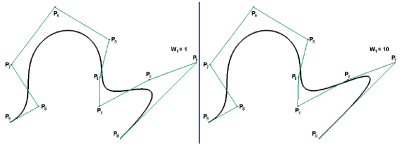
RYS. 7
Podsumowując cykl rozważań na temat krzywych trzeba powiedzieć, że:
-
krzywą Béziera stosujemy wtedy, gdy można spełnić wymagania konstrukcyjne, a wynikowy stopień krzywej nie jest większy od 15 (w praktyce maksymalnie 7-9);
-
modyfikacja dowolnego punktu kontrolnego krzywej powoduje globalną zmianę jej kształtu;
-
stopień krzywej (d°) zależy tylko od liczby jej punktów kontrolnych;
-
sklejona z kilku krzywych Béziera krzywa typu B-Spline zapewnia ciągłość typu G2 i ?w miarę lokalne? modyfikacje;
-
stopień krzywej B-Spline nie zależy jedynie od liczby punktów kontrolnych, ale także od liczby jej krzywych cząstkowych i stopnia tych krzywych;
-
stopień krzywych cząstkowych krzywej B-Spline nie może być mniejszy od d°=3, bo tylko wtedy można zapewnić ciągłość G2;
-
jeśli krzywa B-Spline zostanie zredukowana do jednej krzywej Béziera i dodamy ?współczynniki wag? punktów kontrolnych, to otrzymamy krzywą typu Rational Bézier (Rys. 8);
-
krzywe typu NURBS, jako uogólnienie krzywych Béziera i B-Spline zapewniają największą swobodę konstrukcyjną, ale trzeba pamiętać, że algorytmy obliczeniowe są bardziej skomplikowane niż dla krzywych Béziera lub B-Spline…
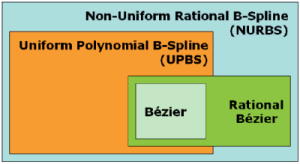
RYS. 8
W kolejnych odcinkach cyklu kontynuacja tematu w zakresie modeli powierzchni oraz odpowiedź na pytanie: czy ta teoria jest potrzebna w praktyce konstrukcyjnej?
Autor: TEKST I RYSUNKI: ANDRZEJ WEŁYCZKO





