Elementarz modelowania powierzchniowego (cz. I)

Ewolucja systemów CAD powoduje, że konstruktor znajduje w nich coraz częściej takie funkcje, które umożliwiają definiowanie inteligentnych i parametrycznych obiektów geometrycznych. Parametrycznych, bo definicja oraz modyfikacja geometrii odbywa się przez zmianę wartości parametrów, a nie przez bezpośrednią ingerencję w model matematyczny. Inteligentnych, bo w modelach asocjatywnych, a takie są definiowane w większości dzisiejszych systemów CAD, zmiana jednego obiektu geometrycznego pociąga za sobą stosowne zmiany we wszystkich obiektach od niego zależnych

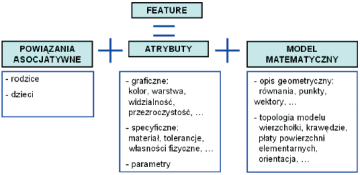
Taka struktura modelu przestrzennego nabiera szczególnego znaczenia w przypadku modeli powierzchniowych, bo użytkownik systemu CAD widzi w coraz mniejszym stopniu model matematyczny krzywej lub powierzchni. To, co jest zaletą systemów klasy Feature-Based Design (Rys. 1), a więc odejście od czysto matematycznego opisu geometrii (stopień krzywej, kierunki główne powierzchni, sieć punktów kontrolnych, itp.) w kierunku pracy z cechami konstrukcyjnymi (feature), parametrami oraz asocjatywnie powiązanymi elementami zależnymi powoduje, że konstruktor nie zawsze zdaje sobie sprawę z tego, jak jego decyzje projektowe wpływają na geometryczną jakość finalnego modelu powierzchniowego projektowanej części. Obiekty projektowe mogą mieć kilka różnych reprezentacji graficznych, a to co widzimy na ekranie komputera nie musi być w pełni zgodne z wymaganiami konstrukcyjnymi nawet, jeśli na pierwszy rzut oka wydaje się nam poprawne.

RYS. 1

Matematyczna część opisu krzywej lub powierzchni zawiera zazwyczaj definicje geometrii i topologii obiektu. Definicja geometryczna to kształt i położenie w przestrzeni 3D, czyli model matematyczny (równania kanoniczne lub parametryczne), punkty charakterystyczne, wektory lub kąty. Element topologiczny opisu matematycznego zapewnia poprawne powiązanie obiektów geometrycznych, czyli ich orientację oraz warunki brzegowe, na przykład zgodność wierzchołków lub styczność wzdłuż krawędzi.

Dla większości konstruktorów, którzy tworzą modele powierzchniowe w systemach 3D jest rzeczą zupełnie oczywistą, że powierzchnia jest tak dobra, jak dobre są krzywe zastosowane do jej definicji. Jeśli dysponujemy krzywymi złej jakości i zastosujemy te krzywe do definicji powierzchni, to oczywiście rezultat będzie również złej jakości. Dlatego tak ważne jest, aby konstruktor dysponował w systemie CAD nie tylko narzędziami do modelowania przestrzennego krzywych lub powierzchni, ale także możliwościami analizy ich jakości.

Mówiąc „dobra krzywa” musimy zdefiniować, czym różni się dobra krzywa od złej krzywej. Pierwszym kryterium oceny jakości krzywej jest jej ciągłość. W teorii modelowania przestrzennego mówimy o czterech rodzajach ciągłości:

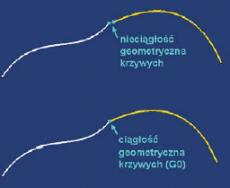
• Ciągłość geometryczna (G0): dwie krzywe mają wspólny punkt początkowy lub końcowy, a dwie powierzchnie mają wspólną krawędź. Jeśli dwie krzywe elementarne nie są ciągłe, to należy zmodyfikować odpowiednio punkt końcowy przynajmniej jednej z nich (Rys. 2).

RYS. 2

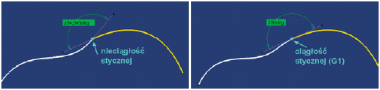
• Ciągłość styczności (G1): dwie krzywe ciągłe według kryterium G0 są wzajemnie styczne w punkcie wspólnym, a dwie powierzchnie ciągłe według kryterium G0 są wzajemnie styczne w każdym punkcie krawędzi wspólnej. Kąt pomiędzy kierunkami stycznymi do obu krzywych w punkcie wspólnym może mieć wartość 0° lub 180°. Jeśli dwie krzywe elementarne nie są styczne, to należy odpowiednio zmodyfikować kierunek styczności przynajmniej jednej z nich w punkcie wspólnym (Rys. 3).

RYS. 3

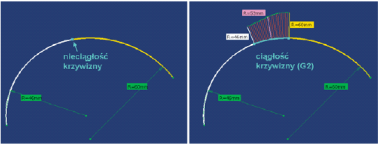
• Ciągłość krzywizny (G2): dwie krzywe ciągłe według kryterium G1 mają taki sam promień krzywizny w punkcie wspólnym.

Klasycznym przykładem nieciągłości krzywizny jest przypadek dwóch łuków okręgów o różnym promieniu – w punkcie wspólnym tych krzywych promień krzywizny zmienia się skokowo, a ciągłość krzywizny oznacza, że nie ma skokowych zmian promienia krzywej. Jeśli dwie krzywe elementarne nie maja ciągłości krzywizny, to w obszarze przyległym do punktu wspólnego należy zdefiniować krzywą „przejścia”, która zapewni ciągłość zmian promienia krzywej (Rys. 4).

RYS. 4 

• Ciągłość gradientu zmian krzywizny (G3): dwie krzywe ciągłe według kryterium G2 mają w częściach przyległych do punktu wspólnego podobny charakter (gradient) zmian krzywizny.

Oczywiście dotyczy to tylko takich przypadków, w których analizowana krzywa jest rezultatem połączenia kilku innych krzywych, bo z definicji algorytmy definiowania krzywej elementarnej w systemach CAD gwarantują jej ciągłość. W każdym systemie CAD krzywa elementarna, czyli taka, która jest opisana jednym równaniem lub układem równań parametrycznych, jest zawsze ciągła – zazwyczaj według kryterium G2. Może się jednak zdarzyć, że krzywa będąca rezultatem zastosowania jakiegoś polecenia, pomimo tego, że jest jednym obiektem w modelu CAD, składa się z kilku krzywych elementarnych – na przykład krzywa przecięcia dwóch powierzchni. Każda z tych krzywych elementarnych ma ciągłość typu G2, ale pomiędzy krzywymi elementarnymi może być zachowana tylko ciągłość G1 lub nawet G0. Możliwe jest też, że to konstruktor zdefiniuje kilka krzywych elementarnych, które potem zamierza ze sobą połączyć w jeden obiekt. Właśnie dlatego analiza ciągłości krzywej jest na etapie definiowania elementów bazowych nowotworzonej powierzchni niezbędna.

Oczywiście nie każdy system CAD oferuje wszystkie wymienione wyżej rodzaje ciągłości. Trzeba też dodać, że ciągłość typu G3 jest wymagana w wyjątkowych zastosowaniach, na przykład przy projektowaniu karoserii niektórych typów samochodów i dlatego, nawet jeśli system CAD pozwala uzyskać ciągłość typu G3, to nie można oczekiwać, że każda krzywa, która posłuży do definicji powierzchni, musi mieć najwyższy z dostępnych rodzaj ciągłości. W większości zastosowań ciągłość typu G2, a niekiedy tylko G1 zapewnia spełnienie wymagań konstrukcyjnych.

Opisane wyżej problemy ciągłości krzywych pozwalają rozwiązać narzędzia typu Curve Connect Checker (Rys. 5). Użytkownik systemu musi jedynie wskazać krzywą lub zestaw krzywych, a następnie dla wybranego typu analizy (Distance = ciągłość G0, Tangency = ciągłość G1 lub Curvature = ciągłość G2) ustalić dokładność (tolerancję) analizy.

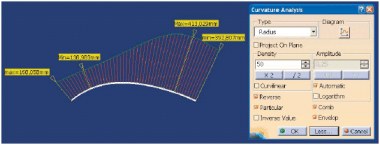
RYS. 5

Na przykład, jeśli dla typu Tangency użytkownik zada wartość 0,5°, to pomiędzy krzywymi, których kierunki styczne w punkcie wspólnym mają kąt większy od 0,5° system oznaczy punkt nieciągłości według kryterium G1 (Rys. 6). Podobnie dwie krzywe, których kierunki styczne w punkcie wspólnym mają kąt mniejszy lub równy 0,5° będą oznaczone jako ciągłe według kryterium G1. Takie inżynierskie, bo oparte na zdefiniowanej przez użytkownika tolerancji, podejście do zagadnień analizy i oceny jakości modelu geometrycznego przypomina konstruktorowi, że w świecie rzeczywistym nie zawsze jest potrzebna bezwzględna ciągłość.

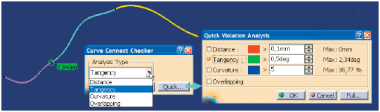
RYS. 6

Teoretycznie bezwzględna ciągłość może być uzyskana po zastosowaniu innego typu funkcji, odpowiedniej metodologii projektowania lub zmianie warunków brzegowych zastosowanych w definicji krzywych elementarnych. Rolą konstruktora jest, aby w oparciu o swoje doświadczenie i rezultat analizy wygenerowanej przez system CAD zaakceptować zgodność modelu geometrycznego z założeniami i wymaganiami projektowymi lub podjąć odpowiednie decyzje projektowe, aby zapewnić wymaganą ciągłość krzywych.

Spełnienie warunków ciągłości krzywej nie musi jednak oznaczać, że jest ona najlepsza z możliwych. Analiza ciągłości krzywej poprzedza zazwyczaj kolejny typ analizy: rozkład zmian krzywizny wzdłuż krzywej (funkcja Porcupine Curvature Analysis). To narzędzie stosujemy do wykrywania niepożądanych zmian krzywizny, szczególnie takich miejsc na krzywej, w których krzywizna zmienia znak, a które z racji swojego lokalnego charakteru nie są widoczne gołym okiem. Inaczej mówiąc, rezultatem analizy typu Porcupine Curvature Analysis jest wizualizacja przebiegu zmian krzywizny lub promienia krzywizny krzywej oraz identyfikacja punktów przegięcia krzywej (Rys. 7). To właśnie w tych punktach promień zmienia znak, a krzywa, która zazwyczaj powinna mieć ciągły i w miarę monotoniczny charakter zmian krzywizny, ma niepożądane lokalne minimum lub maksimum. Interpretacja wyników takiej analizy jest bardzo intuicyjna. W każdym punkcie analizowanej krzywej system oblicza promień krzywizny i generuje odcinek linii prostej prostopadły do krzywej w tym punkcie o długości proporcjonalnej do obliczonego promienia krzywizny. Gęstość i długość prążków może być w łatwy sposób skalowana, aby wyraźnie zobaczyć przebieg zmian promienia krzywizny, który dodatkowo może być pokazany w postaci obwiedni poprowadzonej przez punkty końcowe prążków.

RYS. 7

Punkty przegięcia analizowanej krzywej łatwo zidentyfikować, bo są to punkty, w których obwiednia krzywizny przecina analizowaną krzywą. Oczywiście może być tak, że krzywizna w sposób zamierzony zmienia znak wzdłuż krzywej, dlatego należy jasno powiedzieć, że funkcja Porcupine Curvature Analysis ułatwia jedynie analizę zmian krzywizny, ale to konstruktor decyduje, czy akceptuje kształt krzywej. Na przykład na Rys. 8 krzywa pokazana po lewej stronie ma zbyt wiele (niepotrzebnych!) punktów przegięcia, a krzywa po prawej stronie, chociaż „na oko” bardzo podobna do tej po lewej stronie, ma tylko tyle punktów przegięcia, ile potrzeba do poprawnego zdefiniowania charakteru krzywej.

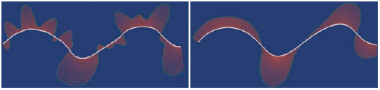
RYS. 8

Modyfikacje krzywej można przeprowadzać przez stosowne zmiany jej elementów nadrzędnych (rodziców) – na przykład współrzędnych punktów bazowych krzywej typu Spline lub stosując lokalnie wygładzanie krzywej w celu uzyskania ciągłości zadanego typu (Rys. 9).

RYS. 9

W tym celu można posłużyć się funkcją Curve Smooth (Rys. 10), która poza możliwością wyboru kryterium wygładzania (Point, Tangent lub Curvature, czyli odpowiednio G0, G1 lub G2)) umożliwia zdefiniowanie maksymalnej deformacji krzywej oryginalnej (Maximum deviation). Rodzaj ciągłości przed „wygładzeniem” jest podany w linii In (Input) a po „wygładzeniu” w polu Out (Output). Co więcej, jeśli nie jest możliwe takie wygładzenie krzywej, aby spełnione były wszystkie zdefiniowane wymagania (np.: Maximum deviation = 0,01mm i Continuity = Curvature), to system sygnalizuje to przez czerwone tło opisu lub żółte, kiedy możliwa jest tylko częściowa poprawa geometrii (np.: uzyskanie ciągłości typu G1, ale nie G2).

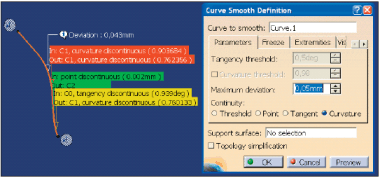
RYS. 10

Na zakończenie części dotyczącej krzywych kilka wniosków:

1. Ocena jakości krzywej nie może być wykonywana jedynie wzrokowo.

2. Analiza jakości krzywej (ciągłość i rozkład krzywizny) powinny być nieodłącznie związane z definiowaniem krzywych.

3. Dobre krzywe są podstawą dobrej jakości powierzchni.

W kolejnym numerze Design News kontynuacja tematu w zakresie analizy jakości powierzchni.

Autor: TEKST I RYSUNKI: ANDRZEJ WEŁYCZKO